Milestone 3
Goals
The purpose of this milestone was to overhaul our robot’s top-level decision making while navigating through a sample maze. While in the past our robot was capable of right-hand wall following and other simple path-following algorithms, we focused on efficient maze exploration this week by implementing a depth-first search algorithm.
Materials
No additional materials were implemented for this Milestone.
DFS (Overview)
Depth-first search is an algorithm used to traverse the nodes of tree and graph structures by ‘visiting’ each node. In a depth-first search, the next node to visit is selected by determining which adjacent nodes have not been visited yet, selecting one node, and travelling there, repeating the process on arrival. In the below graphic, the nodes in the graph are numbered in the order that a DFS will visit them:
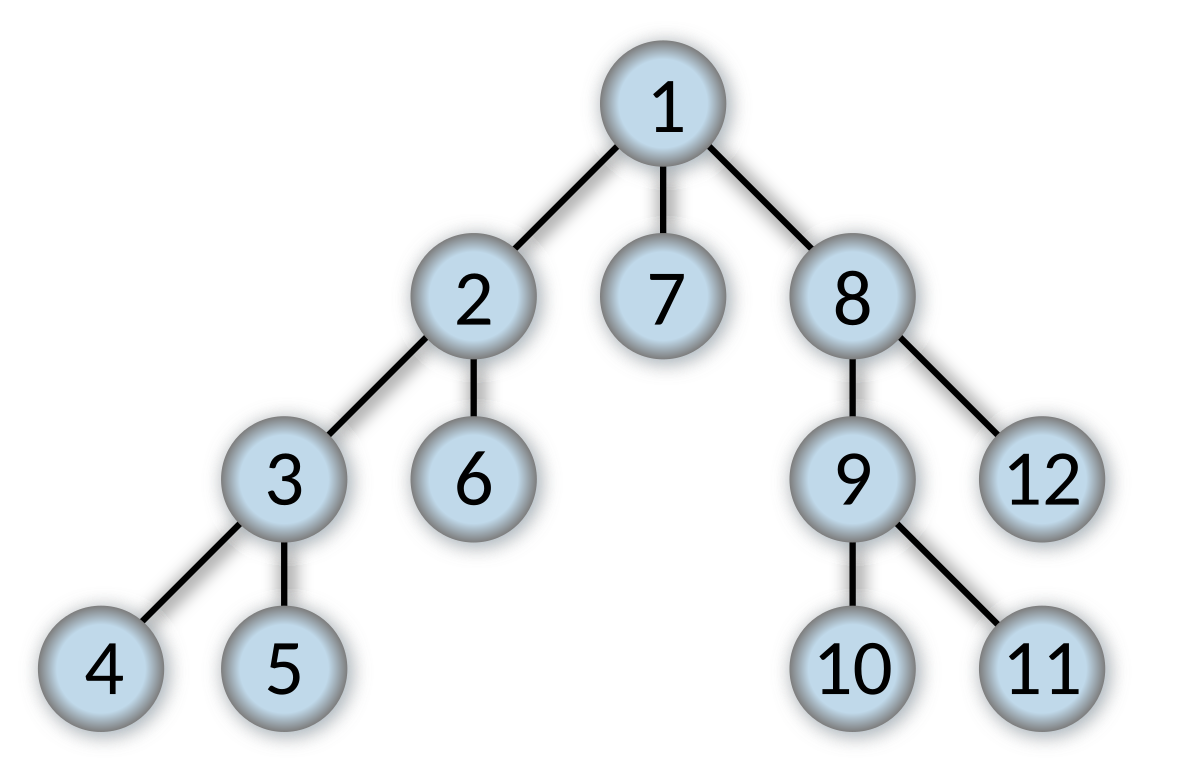
On the maze, our robot will appear to work it’s way into a nook of the maze before backtracking and exploring an adjacent nook, and repeating this process until the entire maze has been traversed.
We decided to implement a depth-first search (DFS, henceforth) algorithm because our system’s available memory is becoming increasingly constrained, and DFS has the smallest memory footprint of the possible traversal schemes (DFS, BFS, Shortest Path, or A*).
Implementation
On our robot, we use a recursive DFS algorithm. We chose to implement DFS recursively because an iterative implementation would require the creation of a stack data type, that could potentially be costly in terms of memory usage. The recursive implementation in effect uses recursive function calls as a sort of stack, allowing us to save on memory.
Now, our robot is controlled by a DFS maze exploration algorithim that is called at each intersection of the maze. The algorithm essentially consists of 3(ish) stages, which are as follows:
Stage 0: Mark Space as Visited Indicate that the space the robot currently occupies has been visited
Stage 1: Figure out Movement Options The robot reads the wall values and uses these to determine which directions it can move in. the cardinal direction of these movement options (e.g. N, E, S, W) is recorded.
Stage 2: Explore Movement Options for each movement option, the robot will determine which way it needs to turn (if at all) to travel in that direction. it will then move in that direction and call dfs recursively from the next intersection it reaches.
Stage 3: Backtrack the robot orients itself in the direction opposite to the direction it was facing when DFS was called. it then drives back to the intersection that dfs was called from.
In order to debug this implementation, we first mocked this algorithim up in MATLAB. From this, we obtained the following animation of the robot’s traversal:

In practice, the robot behaves in essentially the same way.
DFS with Maze, but no GUI
DFS with Smaller Maze and GUI